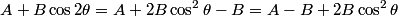 This is the intensity one would get if the incident light consisted of 1) light with intensity 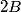 polarized along polarized along 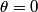 and 2) unpolarized light with intensity and 2) unpolarized light with intensity 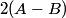 . In order to be able to add the intensities as we have done, we need to assume that parts 1) and 2) are incoherent. %(see Giancoli page 873-874 and 877). . In order to be able to add the intensities as we have done, we need to assume that parts 1) and 2) are incoherent. %(see Giancoli page 873-874 and 877). Assuming this, then answer (C) is correct. |